1.晶体结构与X射线衍射
晶体结构
1. Bravais晶格
重复结构的空间位置代表点组成的空间点阵叫做晶格,空间代表点称为格点,空间的重复结构称为基本单元,简称基元。各基元之间位置等价,即站在任何一个基元上看到的风景完全一样,根据数学理论,布拉格格子只有14种。
2. 基矢
三个不共面连接相邻格点的矢量称为基矢 \[ \{ R = n_1a_1+n_2a_2+n_3a_3|n_1,n_2,n_3 \in Z \} \]
3. 原胞
以晶矢为三边组成的平行六面体晶胞称为原胞,体积最小,只包含一个格点。
Wigner-Sietz原胞:以任一格点为中心,作它的最近邻,次近邻等格点的垂直平分面,由这些面所围成的最小封闭多面体也满足原胞的要求,称为 Wigner Sietz原胞。
4. 典型结构
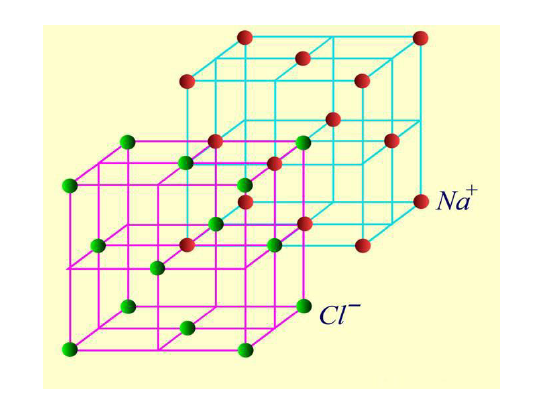
基元为一个钠离子和一个氯离子,为面心立方格子。
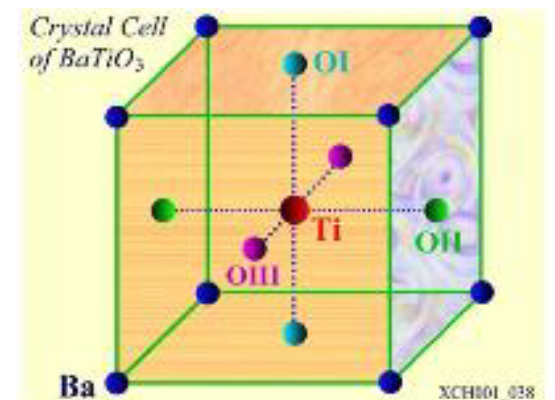
基元为一个Ba离子和一个Ti离子和三个O离子,为简单立方格子。
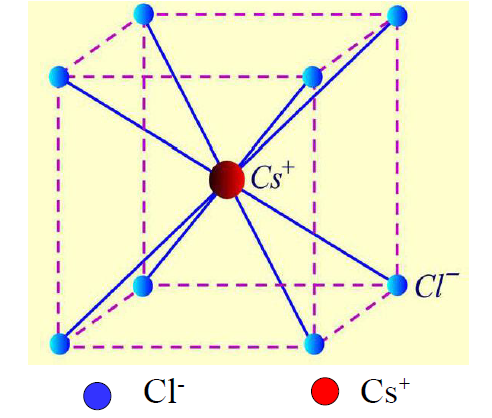
基元为一个Cs离子和一个Cl离子,为简单立方格子。
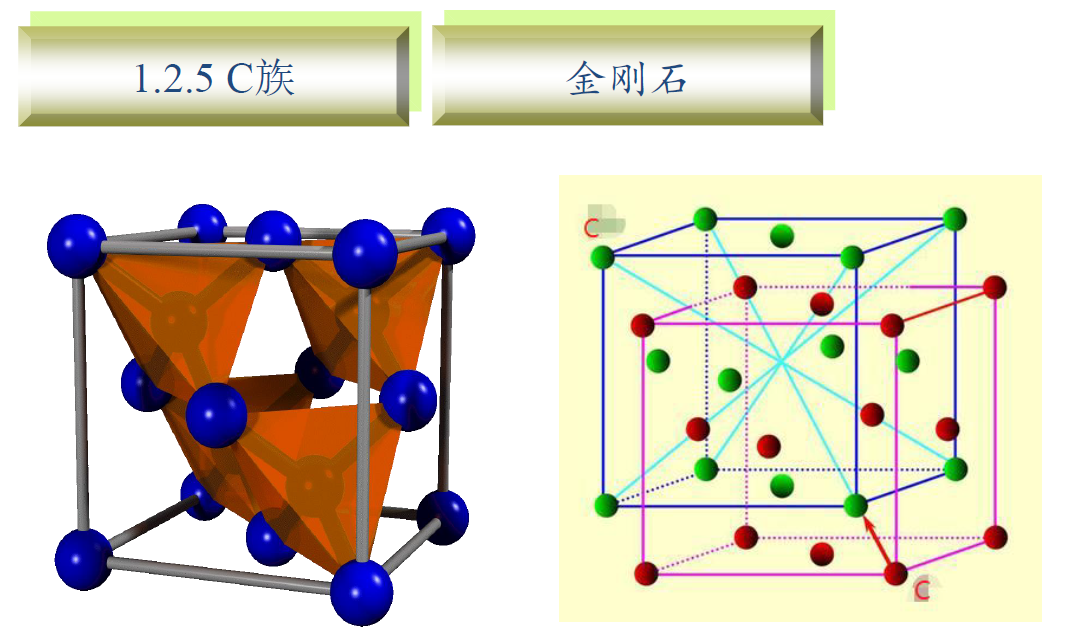
闪锌矿也是这种结构,基元为晶胞内的一个C加上体心或角上的一个C,为面心立方格子。
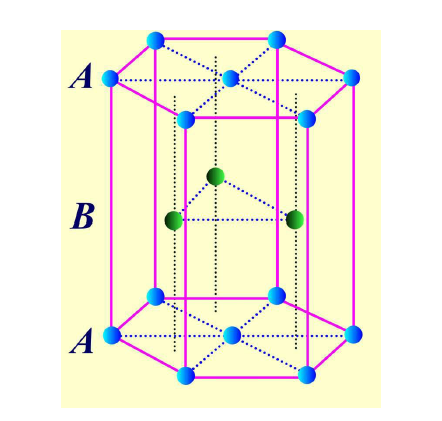
体心内的C和表面的C不等价,原因是最近邻的C原子构成的棱柱方向不一样,所以这两构成基元,布拉菲格子为简单六方。
5. 晶面指数
取定原点和晶矢之后,某个面与坐标轴的交点为\((h_1,0,0),(0,h_2,0),(0,0,h_3)\),则与此平行的任何面在物理上是平移不变的,则\((1/h_1,1/h_2,1/h_3)\)称为这一族晶面的晶面指数。
6. 对称和空间群
旋转对称性:旋转\(2\pi/n\)后恢复原状,则用\(n,C_n\)表示
反演对称:关于某个点晶胞取反后\((x,y,z) \rightarrow_{(0,0,0)} (-x,-y,-z)\)晶胞不变,用\(i,C_i\)表示
镜面对称:关于某个面晶胞取反后\((x,y,z) \rightarrow_{(x,y,0)} (x,y,-z)\)晶胞不变,用\(m,\sigma\)表示
象转对称:旋转和反演对称的结合,先旋转\(2\pi/n\)后关于某点反演对称后晶胞不变,用\(\bar{n}\)表示
晶体点群23种,加上平移230种。
7. 倒格子
定义倒格子的基矢\(b_i = \frac{2\pi}{V}\epsilon_{ijk}(a_j\times a_k)\),\(V\)为正格子体积,\(a_i\)为正格子基矢,则三个基矢张成了整个倒格子空间。
7.1 theorem: 倒格矢 \(\{G=h_1b_1+h_2b_2+h_3b_3|k_1,k_2,k_3 \in Z\}\), 与晶面 \((h_1,h_2,h_3)\) 正交,且晶面之间的间隔 \(d = 2\pi/||G||\)
prove:
\(g = h_1b_1+h_2b_2+h_3b_3\),\(\frac{1}{h_1}a_1-\frac{1}{h_2}a_2, \frac{1}{h_2}a_1-\frac{1}{h_3}a_3\)与晶面\((h_1,h_2,h_3)\)平行,
\[ g \cdot (\frac{1}{h_1}a_1-\frac{1}{h_2}a_2)= (h_1b_1+h_2b_2+h_3b_3) \cdot (\frac{1}{h_1}a_1-\frac{1}{h_2}a_2) \]
\[ = a_1 \cdot b_1 - \frac{h_1}{h_2}a_2\cdot b_1 +\frac{h_2}{h_1}a_1\cdot b_2 -a_2\cdot b_2 + (\frac{1}{h_1}a_1-\frac{1}{h_2}a_2) \cdot b_3 \]
\[ = 2\pi - 0 + 0 - 2\pi + 0 = 0 \]
同理\(\frac{1}{h_2}a_1-\frac{1}{h_3}a_3\)。
取所有倒格矢的垂直平分线,离\((0,0,0)\)最近的被分割出的区域称为第一布里渊区,次近为第二布里渊区...
8. X衍射
8.1 Laue方程:
假设为弹性散射,\(k_0\)为入射波,\(k\)为出射波,G为倒格矢,满足Laue的出射波会得到加强。
\[ k - k_0 = G \]
8.2 Bragg公式:
布拉格把原子晶面当成镜面推导出了加强衍射的公式
\[ 2d sin \theta = n \lambda \]
d为晶面间距离,\(\theta\)为波矢和晶面的夹角。
两者等价性推导:

已知\(k - k_0 = G\),显然G垂直于一组晶面并且晶面间距\(d = \frac{2\pi}{|G|}\)如图,
\[ \begin{aligned} &k \cdot G = - |K||G|cos(\frac{\pi}{2}+\theta) \\& lhs = (G+k_0) \cdot G = G^2 +k_0 \cdot G = G^2 + |k||G|sin(\theta) \\& rhs = - |k||G|sin(\theta) \end{aligned} \]
第一行来源于几何关系,第二行来源于Laue方程,第三行来源于弹性散射假设。
\[ \begin{aligned} & \therefore 2 |k|sin(\theta) = |G| \\&\because d = 2n\pi/|G| |k| = 2\pi/\lambda \\&\therefore 2dsin(\theta) = n\lambda \end{aligned} \]
7.3 散射因子
原子散射因子公式:\(f(K) = \int_{r}{e^{iKr}\rho(r)dr}\), \(\rho\) 是电子密度,\(K\)是波矢的变化量,积分范围为原子电子云的区域,\(f\)描述单原子散射后的光振幅\(Af\)。
几何结构因子:\(S(K) = \Sigma_{j=1}^{s} f_j(K)e^{i K \cdot r_j}\), 就是散射的是晶体的话,算散射振幅和加强点时,需要对晶胞内的所有原子散射因子按照公式进行叠加,\(f_i,r_i\)是原子的散射因子以及对于晶胞原点的位矢,\(S\)描述晶体散射后的光振幅\(ASN\),N为晶胞个数。
习题
- 证明理想六方最密堆积结构中\(c/a=1.633\), a为六边形边长,c为高

位于中间层的原子和底层的对应的三个原子形成一个正四面体:该正四面体的高度为\(h = \sqrt{a^2-(\frac{a}{\sqrt{3}})^2}\),而上下对称所以\(c = 2h\)
- 若晶胞晶矢\(a_1, a_2, a_3\)相互垂直,试求晶面族\((h,k,l)\)的面间距
面间距 \(d = 2\pi/|G| = 2\pi/|hb_1+kb_2+lb_3|\),因为正格矢相互正交,
\[ a_i \times a_j = \epsilon_{ijk} |a_i||a_j|a_k/|a_k| = b_k \frac{V}{2\pi} \]
\[ \therefore \frac{2\pi}{|a_i|^2} a_i = b_i \] 所以
\[ |G| = \sqrt{(hb_1)^2+(kb_2)^2+(lb_3)^3} \]
\[ = 2\pi \sqrt{(h/a_1)^2+(k/a_2)^2+(l/a_3)^2} \]
\[ \therefore d = \frac{1}{\sqrt{(h/a_1)^2+(k/a_2)^2+(l/a_3)^2}} \]
- 在体心立方的晶胞的每个面中心加上一个同类原子,问该种结构的布拉菲格子和基元是什么?
基元应当取为三个面心和体心和一个角上的原子共5个,布拉菲格子为简单立方。
- 试求面心立方结构的\((1 1 1)\)和\((110)\)面的原子面密度
\((1,1,1)\)面截面大小\(S = \frac{\sqrt{3}}{4}(\sqrt{2}a)^2 = \frac{\sqrt{3}}{2}a^2\),原子个数\(\frac{1}{6}*3 +\frac{1}{2}*3\) , \(\rho = \frac{4}{\sqrt{3}a^2}\)
\((1,1,0)\)面截面大小\(S =\sqrt{2}a^2\),原子个数\(\frac{1}{4}*4 +\frac{1}{2}*2\) , \(\rho = \frac{\sqrt{2}}{a^2}\)
试求金刚石的散射因子,并讨论X射线衍射消失的条件
记忆金刚石的结构方法:面心立方,加上四根对角线的四分之一处各有一个C,其中左边右边各有两个,往x-y平面的投影不可能重叠。
金刚石结构中共有八个原子, 对应的坐标为(基矢为晶矢)
\[ (0,0,0),(1/2,1/2,0),(0,1/2,1/2),(1/2,0,1/2) \]
\[ (1/4,1/4,1/4),(3/4,1/4,3/4),(3/4,3/4,1/4),(1/4,3/4,3/4) \]
几何结构因子:
\[ S(k) = \sum_i {f_i e^{i k\cdot r_i}} \]
求和i表示对所有原子求和,由于边缘上的原子只能代表“分数个”原子,所以往往由空间周期性把“分数个”原子移到某个位置凑整。
\[ S(k) = (1+e^{ia(k_x+k_y)/2}+e^{ia(k_y+k_z)/2}+e^{ia(k_x+k_z)/2})(1+e^{ia(k_x+k_y+k_z)/4}) \]
所以消光条件为:\(k_x+k_y+k_y = \frac{4\pi}{a}\) or 第一项表达式为0(网上答案不对,这里并没有要求\(k_i\)是波矢的整数倍)