Z2规范场论的minimal的知识
规范理论
量子力学中的模型由两部分构成,第一部分是系统演化的哈密顿量 \(H\), 第二部分是系统存在的希尔伯特空间 \(\mathcal{H}\),往往只需要取态能够存在的空间作为 \(\mathcal{H}\) 就足够分析使用,比如粒子生活在周期性的势场中\(H = P^2/2m +V\cos(2\pi x/a)\), 由于势场是有周期平移对称性的,猜测应当也具有周期平移的态才合法,定义变换 \(T_a \psi(x)=\psi(a+x)\), 于是取\(\mathcal{H}_a=\{\psi|\psi\in L^2[-\infty,+\infty], T_a \psi = \psi \}\), 这个空间就够了。
但是在有的情况下, 在全局的\(\mathcal{H}\)下定义是有用的,比如该粒子与另一非周期的粒子存在相互作用, 于是需要扩展到所有平方可积函数作为\(\mathcal{H}\)的成员, 这种情况下去研究问题,就需要引入规范结构, 从而将这个周期的粒子"规范"定义于大的希尔伯特空间中,具体的:
定义变换 \(T_a \psi(x)=\psi(a+x)\)为规范变换,容易得见\(H T_a = T_a H\),哈密顿量与规范变换算符相互对易。
合法的态满足:
\[\left|x+a\right> = \left|x\right>\]
在大希尔伯特空间 \(\mathcal{H}\) 中,并非每个态都是满足以上条件,故为了表示在 \(\mathcal{H}_a\) 以外的态,需要多添加一个数用于标记,比如 取定了一套\(\left|x\right>\)坐标基矢,则在大希尔伯特空间 \(\mathcal{H}\) 中 任意态写作:\(\psi(x) = \left<\psi|x\right>\), 取 \(n\) 为任意整数,在 \(n\) 次 \(T_a\) 作用于态\(\psi\) 后,任意态写作:\(\psi'(x) = \left<\psi T_a^n|x\right> \ne \left<\psi|x\right>\),也就是在 大空间上的作用并非平凡的,而作用于\(\mathcal{H}_a\)上的态 \(\psi'(x) = \left<\psi T_a^n|x\right> = \left<\psi|x\right>\) ,于是可以用\(n=0\) 代表并未对态做过规范变换,\(n\)表示对态做规范变换的次数, 这样就可以在大的空间中用\(\psi_a \in \mathcal{H}_a\) 和一个多余的数 \(n\) 来标记某个态, 这样的处理方式让描述系统的空间扩大且多了一个自由度,这样的结构称为规范结构 ,同时将周期平移对称性隐含在了规范结构中,有时也称这个系统拥有了规范对称性, 当然多个对称性的系统也可以这样的处理,同时用 \(\{n_1,n_2,..n_k\}\) 矢量(gauge sector)来标记系统, 在这个例子中,规范矢量满足整数群Z的对称性,故称这个系统满足整数群Z的规范对称性。
\(n\) 在只讨论 \(\mathcal{H}_a\) 内的态时时不会产生任何的意义,只有当出现了规范破坏的项, 也就是不满足对应的对称性的项出现时,矢量才有意义。同时,各个物理量也必须满足规范变换下不变, 系统才能是规范不变的。
纯 \(Z_2\) 格点规范理论
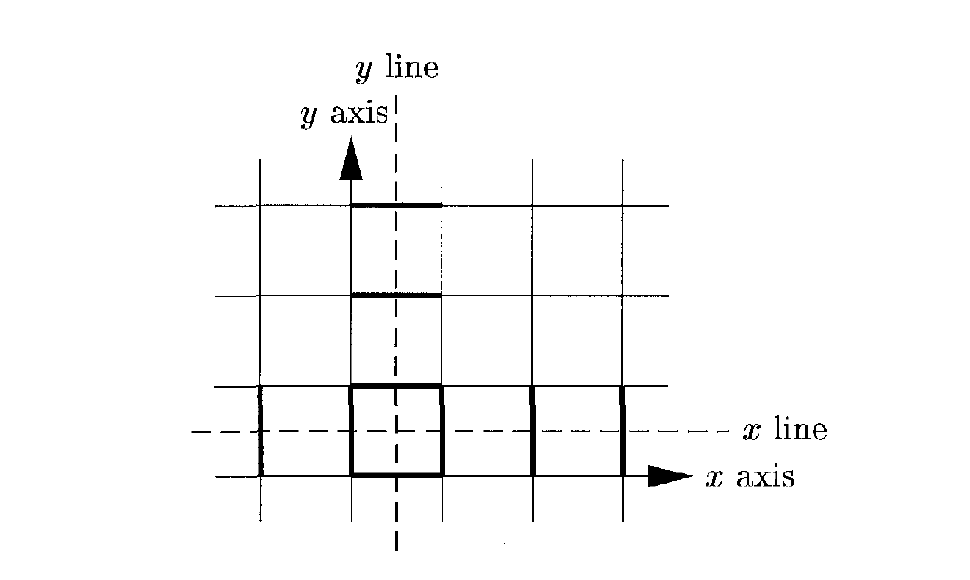
单纯的\(Z_2\)系统定义在二维周期边界条件阵列上,在每个棱上有一个场\(s_{ij}\)(比特), \(i,j\)为与其相连的格点,其满足传统二能级结构,也就是说: 系统的大希尔伯特空间可以有\(\left|++--...\right>\)的形式表达出来, 其中每个比特位对应某条具体的棱, 但是当我们引入某种规范结构,即限制整个二维网的构型到某个子空间中(即小希尔伯特空间),可以在这种 限制下得到某些奇特 的性质,同时也可以探究出哈密顿量的具体形式以及在背后的对称性。
这里用格点定义规范变换\(G_i\),定义为对与\(i\)格点相连的场进行翻转 \(s_{ij} -> -s_{ij}\),并且认为\(G_i\)作用 后的系统与原系统完全一致,没有任何区别,在这样的规范变换定义下,假定 初始状态下\(W_i = 1,\forall i\in lattice\), 则对于格点的函数 \(G_i = \pm 1\),都对应于一个规范变换,\(W_i \rightarrow W_iG_i\),于是\(W_i\)成为了 这个规范变换的gauge sector,与格点一一对应,同时每个格点的矢量\(W_I\)满足\(Z_2\)对称性,称为 \(Z_2\) 规范场。
命题1 规范变换下,量\(F(C)=\prod_{\{i,j\} \in C}s_{i,j}\) 是规范不变量。
C是环面上的任意闭合曲线,而任意规范变换一定会是同时操作闭合图形两个棱的翻转,所以这个量在规范变换下 保持不变。
再有,通过这个量可以分别不同的规范变换态,取最小的方格为一个C,则每个方格都可以提供一个用于标记 态的规范自由度的变量,两个构型如果任意一个 \(F(square)\) 不相同,就证明这两个构型是不可能通过规范变换 得到,也就是在子空间中这两个态不相同。
命题2 规范变换下,量 \(\sigma^z_{i,j}\) 是规范不变量。
对某个棱的翻转算符\(\sigma^z_{i,j}\) 与\(W_k\)相互对易,所以命题成立。
z综上所述,\(Z_2\)的哈密顿量必须是规范变换下不变的,最简单的写法可以写作:
\[H = -g \sum_i^{\text{square}} \prod_{(l,m) \in i} \sigma_{x,(l,m)} -t \sum_{(k,g)} \sigma_{z,(k,g)}\]
最后讨论一下子空间中的拓扑简并态, 假设系统有 \(Nx \times Ny =N\) 个格点且满足\(g \gg t\),并且满足周期对称条件,那么实际上就有2N根棱,不考虑 规范结构,实际可能有\(2^{2N}\)个态,gauge sector有 \(N\) 个变量,共有\(2^N\)个组合,但是 注意到gauge sector 取 \((1,1,1,1,...)\) 和 \((-1,-1,-1,...)\) 时完全一致,所以有 \(2^N/2\)个有效组合,故子空间里的态应该有\(2\times 2^N\)个,通过\(F(square)\)来标记态的话,拥有 \(N\) 个变量,但是所有的\(\prod_i^{\text{square}} F_i = 1\),也就是说 \(F_i\) 只能提供 \(2^N/2\) 个标记, 最终认为有 \(2^{N+1}/2^{N-1}\) 四个态是完全兼并的,他们的 \(F_i\) 完全相同,\(H\) 的期望值也完全相同 ,在任意局域的\(\sigma^z_i\)的翻转作用下也没有办法解简并。转换方法需要环绕整个系统的线的沿x翻转或者沿y翻转。 这是一个全局的拓扑操作,给甜甜圈切了一刀,改变了系统的拓扑性质,故也称拓扑简并态。
在\(g\gg t\rightarrow 0\) 时,激发是通过翻转某处\(F_i\)实现, 称激发子为\(Z_2\)涡旋,因为\(\prod_i^{\text{square}} F_i = 1\)涡旋必须成对出现且具有全局的纠缠效应, 这个相称为\(Z2\)场的解禁闭相(Deconfined Phases),而当\(t\gg g\rightarrow 0\) 时\(Z2\)场退化为Ising模型 激发局域化,称这个相为禁闭相(Confined Phases)。
\(Z_2\) 格点规范理论与物质的相互耦合
考虑格点哈密顿量:
\[H=\sum_i \mu_i \hat{a}_i^{\dagger} \hat{a}_i\]
观察到格点上的升降算符有对称性 \(\hat a_i \rightarrow -\hat a_i\),并不改变其哈密顿量, 猜测定义局域规范变换为 \(\hat{\mathcal{V}_i}\equiv e^{i\pi\hat{n}}: \left|n\right>\rightarrow (-1)^n\left|n\right>\), 容易验证\(\hat{\mathcal{V}_i} a_i = -a_i \hat{\mathcal{V}_i}\)。
玻色子(为了简洁,省略位点角标):
\[\begin{aligned} \hat{\mathcal{V}} a \hat{\mathcal{V}}^\dagger &= e^{-i\pi a^\dagger a}ae^{i\pi a^\dagger a} \\& = a - (i\pi)[a^\dagger a,a] +(i\pi)^2[a^\dagger a,[a^\dagger a,a]]/2! +\dots \\&= a -(i\pi)(-1)a + (i\pi)^2(-1)^2a/2! + \dots \\&= a (1+i\pi+(i\pi)^2/2!+\dots) \\&= -a \end{aligned}\]
费米子则更为简洁,根据定义\(\hat{\mathcal{V}_i} = \sigma^z\),容易验证\(\{\sigma^z,\sigma^\pm\} = 0\)。 ,进一步可以得到\(\hat{\mathcal{V}_i}H = H \hat{\mathcal{V}_i}\)规范不变,规范变换有意义。 根据前文规范理论,认为规范变换后的态与原态完全一致(实际也满足谐振子模型的基矢相位的任意性), 则得到了这个系统中的gauge sector,每个位点上有一个满足 \(Z_2\) 代数结构的规范对称性, 则可以用\((0,0,0,0,..)\)等\(N\)个数表示未加变换的某个选定的能量本征态上(\(N\) 为格点数), 减少了需要讨论的态的个数。
往往格点之间不相互独立,需要讨论格点间的相互作用时,猜测哈密顿量直接写作:
\[H=J \sum_{\langle i, j\rangle}\left(\hat{a}_i^{+} \hat{a}_j+\text { h.c.}\right)+\sum_i \mu_i \hat{a}_i^{\dagger} \hat{a}_i\]
沿用上文中关于local规范变换的定义,则有:
\[\hat{a}_i \rightarrow \hat{\mathcal{V}_i} \hat{a}_i, \quad \hat{a}_i^{+} \rightarrow \hat{a}_i^{+} \hat{\mathcal{V}_i}^{+}\]
则变换后的哈密顿量写作:
\[H=J \sum_{\langle i, j\rangle}\left(\hat{a}_i^{\dagger} \hat{\mathcal{V}_i}^{\dagger}\hat{\mathcal{V}_j}\hat{a}_j+\text { h.c. }\right)+\sum_i \mu_i \hat{a}_i^{\dagger} \hat{a}_i\]
显然直接耦合的哈密顿量相互作用项并不是规范不变的, 前文的规范变换与此哈密顿量不兼容,需要重新考虑哈密顿量的构造以及规范变换的选取。
考虑在两个格点之间引入额外自由度(某个场) \(\hat{\mathcal{U}}_{\langle i, j\rangle}\), 并且定义其规范变换的规则\(\hat{\mathcal{V}'}_i\),\(\hat{\mathcal{V}'}_i\)的变换规则 需要与物质场的变换规则\(\hat{\mathcal{V}}_i\)相关联,最终让\(H\)在联合的变换下保持不变。
发现,以格点为记号,并且操作只有正负两种选择,操作后认为态并没有发生变化,\(Z2\)纯规范场刚好 符合要求,定义联合操作:
\[\begin{aligned} W_i &= \hat{\mathcal{V}}_i \times G_i \\&= (-1)^{n_i} \prod_{j}^{[i,j]\text{connect}} \sigma_{z,ij} \end{aligned}\]
第一个操作是前文对物质的相位翻转。而第二个操作代表纯\(Z_2\)规范理论中以某格点为中心对场的翻转。
哈密顿量写作:
\[\begin{aligned} H=&J \sum_{[i,j]\text{connect}}\left(\hat{a}_i^{+} \hat{\sigma}^z_{i, j}\hat{a}_j+\text { h.c. }\right)+\sum_i \mu_i \hat{a}_i^{\dagger} \hat{a}_i \\ &-g \sum_i^{\text{square}} \prod_{(l,m) \in i} \sigma_{x,(l,m)} -t \sum_{(k,g)} \sigma_{z,(k,g)} \end{aligned}\]
容易验证\([W_i,H] = 0\),规范变换成立,值得一提的是,物质场能级之间的相位实际上是\(U(1)\)的, 所以\(Z_2\)模型是\(U(1)\)的一个简单类型,如果物质场写成旋量,实际上还能引入\(SU(N)\)等更为广泛的规范场, 这种类型的格点规范场论最基础的也最具有意义。\(Z2\) 规范场作为一种真实物理的简单情况,同时由于自身非禁闭相 的全局纠缠性质在强关联系统以及拓扑纠错等领域具有重要意义。