开放系统,连续测量,随机主方程的一些介绍和个人臆想
量子测量往往需要一个载体,通过纠缠将不容易直接读取的量子态与一个尺度更大,更容易被分辨的系统耦合在一起,通过对大尺度"器材"(光子,电子)的测量从而完成一个量子信息到经典信息的变化。这个过程中量子信息变成经典信息(波函数的塌缩)发生在什么时候是一个经常讨论的问题,涉及到量子力学的诠释问题,此处不予深究。本篇讨论主要想通过连续测量这种 "慢动作的测量过程",来把开放系统和测量过程做一个桥接,并不包含任何创新,都是教科书内容的总结和陈列,以及我个人的一些看法,正如你所见,我不是这方面的专家,如果不赞同或者有什么本质的科学性的 错误,烦请指出。
连续测量以及随机主方程
这部分内容主要来源于书,作者Kurt Jacobs在全书中主要用量子贝叶斯的方式去描述这个测量过程,再引一本[1],这两本书对测量过程的描述都很详尽,值得一读。这里从量子贝叶斯的角度导出随机主方程(其实抄书)。
回到连续测量,这种测量本质上是将一个连续变量\(x\)(比如谐振子的位置动量或者光场的相干态坐标 等物理量)以对某个变量 \(y\)积分的形式读出:
\[d y=\langle X\rangle d t+\frac{d W}{\sqrt{8 k}}\]
假设\(y\)和\(x\)有衔接的系数,无伤大雅地假定为线性的1,于是以上微分等式成立,也就是对x的测量变成了对y的积分过程,同时在实验中,我们并没有观察到绝对平滑的测量曲线的出现,所以引入假定,在任意时刻的微元过程中,不可避免会有一个随机噪声\(dW\)的项出现,假定这个项与观测量y的强度由\(k\)决定。\(k\)越大,噪声对测量结果的干扰越小,反之,则测量结果完全淹没于噪声之中,完成了一次结果丢失的测量过程。同时也假设这个噪声是高斯噪声,满足以下分布:
\[P(d W)=\frac{1}{\sqrt{2 \pi d t}} e^{-(d W)^2 /(2 d t)}\]
当微元时间无限趋向于0时其趋向于白噪声。
贝叶斯统计的意义在于通过测量结果\(dy\)对真实变量\(\left<x\right>\)(或者态\(\rho\))的一次估计,也就是通过随机试验对更新人对某个态的知识(state ofknowledge),这个过程刚好可以用来描述量子测量的过程,简而言之,假设密度矩阵\(\rho\)是人当前对态的认知(state ofknowledge),通过每一次的测量结果\(dy\),对应一个贝叶斯更新的算符(似然函数 likelihood function),从而对密度矩阵用似然函数进行更新,从而描述整个测量过程。这个过程的细节都可以看 of knowledge假设对于收敛的无关性等等细节。这里仅仅介绍基本概念用于主要内容的推导。
假设在某个微元时间内得到了测量的结果\(dy\),则条件概率:
\[P(d y \mid x)=\sqrt{\frac{4 k}{\pi d t}} \exp \left\{-4 k \frac{(d y-x d t)^2}{d t}\right\}\]
这个概率的含义:在噪声存在的假设下,得到\(dy\)的结果推测x可能的分布。用在量子测量过程中,则对应着用x的投影算对密度矩阵的一次更新,定义\(A\)矩阵:
\[\begin{aligned} A(d y) & =\int_{-\infty}^{\infty} \sqrt{P(d y \mid x)}|x\rangle\langle x| d x \\ & =\left(\frac{4 k}{\pi d t}\right)^{1 / 4} \int_{-\infty}^{\infty} \exp \left\{-2 k \frac{(d y-x d t)^2}{d t}\right\}|x\rangle\langle x| d x \\ & =\left(\frac{4 k}{\pi d t}\right)^{1 / 4} \exp \left\{-2 k \frac{(d y-X d t)^2}{d t}\right\}, \end{aligned}\]
则下一时刻的态\(\left|\psi(t+dt)\right>\)正比于\(A\left|\psi(t)\right>\),用\(|\hat{\psi}(t+d t)\rangle\)指代未归一化的态,则:
\[\begin{aligned} & |\hat{\psi}(t+d t)\rangle \propto A(d y)|\psi(t)\rangle \\ & \propto\left\{1-\left[k X^2-4 k X\langle X\rangle\right] d t+\sqrt{2 k} X d W\right\}|\psi(t)\rangle . \\ \end{aligned}\]
再由\(\langle\hat{\psi}(t+d t) \mid \hat{\psi}(t+d t)\rangle=1+8 k\langle X\rangle X d t+\sqrt{8 k} X d W\) 得到归一化系数:
\[(1+8 k\langle X\rangle X d t+\sqrt{8 k} X d W)^{-1/2}\approx 1-4 k\langle X\rangle X d t-\sqrt{2 k} X d W\]
带入得到瞬时薛定谔方程:
\[d|\psi\rangle=\left\{-k(X-\langle X\rangle)^2 d t+\sqrt{2 k}(X-\langle X\rangle) d W\right\}|\psi(t)\rangle\]
写成密度矩阵的瞬时主方程形式:
\[\begin{aligned} & \rho(t+d t)=\rho+d \rho=(|\psi\rangle+d|\psi\rangle)(\langle\psi|+d\langle\psi|) \\ & =\rho+(d|\psi\rangle)\langle\psi|+|\psi\rangle(d\langle\psi|)+(d|\psi\rangle)(d\langle\psi|) . \\ \end{aligned}\]
最终得到:
\[d \rho =-k[X,[X, \rho]] d t+\sqrt{2 k}(X \rho+\rho X-2\langle X\rangle \rho) d W\]
简单可以看出,第一项是决定项,不取决于测量结果,而第二项与测量值和随机噪声相关,接着我将通过inefficient测量进一步解释这个方程的结果。
在物理测量中,完全得到了测量结果是一种理想情况,真实情况往往发生于部分信息的丢失,比如待测信息在用经典光的振幅去完成的整个测量过程,但是实际光在传输到接收仪器之前有可能被其余的物体吸收,从而振幅衰减(电压等信号同理),所以这里对这种非充分测量的物理情况进行刻画(还是抄书TAT)。在这个物理情景中,假设Alice分两段进行了测量:
\[\begin{aligned} d \rho= & -k_1[X[X, \rho]] d t+\sqrt{2 k_1}(X \rho+\rho X-2\langle X\rangle \rho) d W_1 \\ & -k_2[X[X, \rho]] d t+\sqrt{2 k_2}(X \rho+\rho X-2\langle X\rangle \rho) d W_2,\\ \end{aligned}\]
对应的测量结果:
\[d y_i=\operatorname{Tr}[X \rho] d t+\frac{d W_i}{\sqrt{8 k_i}}\]
Alice能够获得\(k_1\)对应的测量\(dy_1\),而对于\(k_2\)对应的\(dy_2\)丢失了,假设Alice的state of knowledge \(\tilde{\rho}\)由以下方程决定:
\[d \tilde{\rho}=-\left(k_1+k_2\right)[X[X, \tilde{\rho}]] d t+\sqrt{2 k_1}(X \tilde{\rho}+\tilde{\rho} X-2\langle X\rangle \tilde{\rho}) d V,\]
\(dV\)是新定义的噪声项,与\(dW_i\)的性质完全相同,
同时为了满足在Alice的方程中和在真实物理的过程中,Alice得到的测量结果是自洽的,也就需要对随机变量 \(dV\)做一些要求,即\(dy_1\)在两套方程中相同:
\[\operatorname{Tr}[X \rho] d t+\frac{d W_1}{\sqrt{8 k_1}} =\operatorname{Tr}[X \tilde{\rho}] d t+\frac{d V}{\sqrt{8 k_1}}=dy_1\]
即:
\[\begin{aligned} d V&=\sqrt{8 k_1}(\operatorname{Tr}[X \rho]-\operatorname{Tr}[X \tilde{\rho}]) d t+d W_1 .\\ \end{aligned}\]
可以看到,除了Alice自身的测量时的噪声项,还多了一项\(\sqrt{8 k_1}(\operatorname{Tr}[X \rho]-\operatorname{Tr}[X \tilde{\rho}]) d t\),虽然这个看似是\(dt\)的决定项,实际上是将一个不断将Alice的方程往真实的方程不断修正的随机项,在真实的物理方程中,\(\sqrt{2 k_2}(X \rho+\rho X-2\langle X\rangle \rho) d W_2\),\(dW_2\) 符号随机且正态分布的演化项,而Alice对此不知情,在下一个时刻里,上一个时间段中的这一部分未知的噪声项导致的误差将会导致\(\sqrt{8 k_1}(\operatorname{Tr}[X \rho]-\operatorname{Tr}[X \tilde{\rho}]) d t\)不为0,从而修正之前对此无知导致的错误,再由于\(dW2\)的正态分布,最终这个随机项也是正态分布,反应在\(dV\)中,\(dV\)的方差会大于\(dW_1\),等效噪声变大。
经过一点简化得到最通常使用的非充分测量的主方程:
\[\begin{gathered} d \rho=-k[X[X, \rho]] d t+\sqrt{2 \eta k}(X \rho+\rho X-2\langle X\rangle \rho) d W, \\ k=k_1+k_2 \quad \text { and } \eta=\frac{k_1}{k_1+k_2} . \end{gathered}\]
得到最终表达式我们可以看出,在连续变量的测量中,系数\(k\)表示相互作用的强度,无论观察者是否获得了系统的信息,这一项都是不可去除的,再由Lindblad主方程(为了方便这里都没写哈密顿量,实际上哈密顿量一阶的微分过程,加上就是了):
\[\dot{\rho}(t)=\sum_{\alpha \geq 1}L_\alpha \rho(t) L_\alpha^{\dagger}-\frac{1}{2}\left\{L_\alpha^{\dagger} L_\alpha, \rho(t)\right\}\]
取\(L = \sqrt{2k}X\),则\(\dot{\rho}(t)= -k[X[X, \rho]] d t\),显然为读取过程中导致的退相干项,同时由\(d y=\langle X\rangle d t+\frac{d W}{\sqrt{8 k}}\),可以看出相互作用的强度越大,面临的随机误差将越大。而\(\eta\)用于表征读出效率,效率越高,观察者获取的信号越多,观察者的观察效应导致系统的演化效应越明显,极限情况下,观察者丢掉了所有信息,\(\eta=0\)则随机主方程退化为Lindblad主方程,也就是说"粗心"的观察者是decoherent的来源。
开放系统以及量子轨迹法
第二部分我将从开放系统出发,得到统一的形式,同时简述量子轨迹法,概括其和测量的关系。在上一则Note里,我简要 概括了用于描述开放系统的一些工具,当然除了一些特殊的强耦合的情况,大部分的系统都可以用Lindblad主方程(以下简称主方程)来描述必要引入随机性,但是在实际的求解过程中,主方程的求解往往是一个对计算资源e指数升高的问题,为了解决这个问题,需要减小计算资源的使用。
考虑到开放系统和测量过程实际上是有一定的关联,换句话来说,开放系统本身可以用一个连续测量用来近似模拟。观察到瞬时薛定谔方程的形式,当初态为纯态的时候经过瞬时薛定谔方程的演化最终得到的结果也必然是一个纯态,纯态的演化很大程度上节约计算机的内存占用,同时测量过程引入的随机变量可以搭配蒙特卡洛的方法去求解,在一定程度上也减少了高维度的动力学计算问题的时间。
量子轨迹方法
这里简单推导相同的形式(继续抄书..从而闭环),首先介绍常规的量子轨迹方法的原理和流程:
通常的Lindblad主方程:
\[\dot{\rho}=-i[H, \rho]+\sum_{k=1}^{d^2} \gamma_k\left(L_k \rho L_k^{\dagger}-\frac{1}{2}\left\{L_k^{\dagger} L_k, \rho\right\}\right)\]
适当改写:
\[\begin{aligned} \rho(t+d t) & =\rho(t)-i[H, \rho(t)] d t-\sum_{k=1} \gamma_k \frac{1}{2}\left\{L_k^{\dagger} L_k, \rho(t)\right\} d t+\sum_{k=1} \gamma_k L_k \rho(t) L_k^{\dagger} d t \\ & =e^{-i H_{\mathrm{C}} d t} \rho(t) e^{i H_{\mathrm{C}}^{\dagger} d t}+\sum_{k=1} M_k \rho(t) M_k^{\dagger} \quad \text { where } \\ H_{\mathrm{C}} & =H-\frac{i}{2} \sum_{k=1} \gamma_k L_k^{\dagger} L_k, \quad M_k=\sqrt{\gamma_k d t} L_k . \end{aligned}\]
再定义\(M_0 =e^{-iH_c t}\),则整个演化过程改写为:
\[\rho(t+d t)=\sum_{k=0} M_k \rho(t) M_k^{\dagger}\]
通过改写,我将整个演化过程改写为了\(dt\)时间内的一次测量,\(M_k\)为对应的测量算符,\(dt\)时间后,末态处于\(M_k\rho(t) M_k^{\dagger}/\mathcal{N}\)的概率等于:
\[p_k = Tr[M_k\rho(t)M_k^\dagger]\]
于是整个动力学演化过程变成了不加选择的测量过程,也就是
\[\rho \mapsto \rho_k=\frac{M_k \rho M_k^{\dagger}}{\operatorname{Tr}\left[M_k \rho M_k^{\dagger}\right]}\]
如果不加处理,将演化过程变成不断的混态叠加的过程,则计算量和直接计算Lindblad方程没有区别,
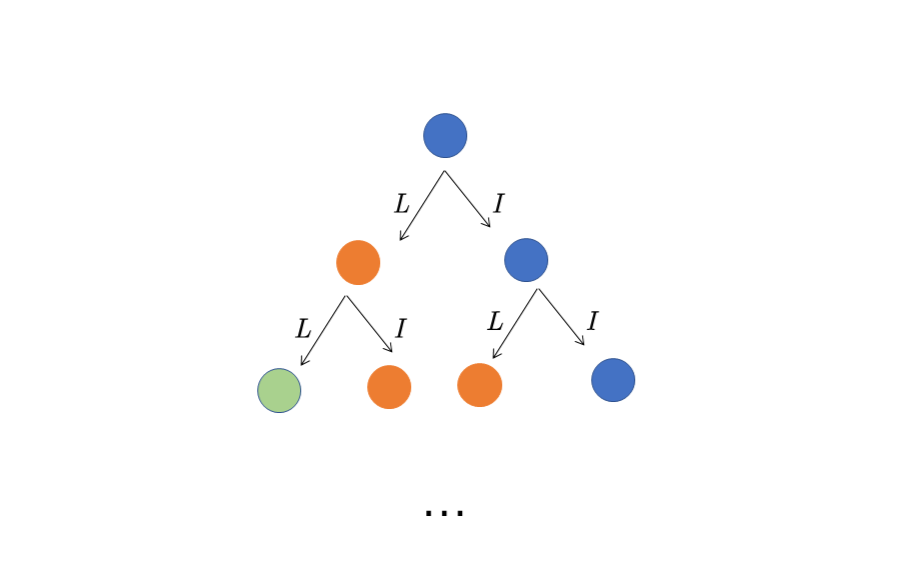
示意图中每个小球代表一个纯态,而从上往下代表时间的增加,每一段单元时间之后态将会演化为同一行小球所共同组成的混态,计算量将会不断增加。这里假设用于模拟这个过程的方式是跳变(quantum jump), 给定初态后,假设每一次以\(p_i= Tr[M_i\rho(t)M_i^\dagger]\)的概率得到下一行中的某个纯态,最终得到了一组\(\{\left|\psi_i(k_1,k_2,k_3,...k_N)\right>\}\),\(k_j\)代表在\(t = j dt\)时刻选择的跳变算符\(P_i(k_1,k_2,k_3,...k_N)= \Pi p_{ki},p_{ki} = Tr[M_{ki}\rho(t)M_{ki}^\dagger]\)。
对于某个想了解的物理学量,求解方式则变为:
\[\left<O\right> = \lim^{}_{N\rightarrow +\infty} \sum^{N}_{i}\left<\psi_i \right|O \left|\psi_i\right>\ \]
态则表示为:
\[\rho = \lim_{N\rightarrow +\infty} \sum^{N}_{i}P_i \left|\psi_i\right> \left< \psi_i \right|\]
则整个过程可以使用蒙特卡洛进行求解。
Lindblad主方程推导随机主方程
受前面的耗散算符可以写成测量算符启发,能不能将Lindblad方程用随机变量的形式改写,统一耗散和测量方程的形式,换句话说,能不能将耗散过程改写成为随机主方程的形式,即:
\[\label{eq1} \mathrm{Av}_{\xi}|\psi(t+\Delta t, \xi)\rangle\langle\psi(t+\Delta t, \xi)|=|\psi(t)\rangle\langle\psi(t)|+\mathcal{L}(|\psi(t)\rangle\langle\psi(t)|) \Delta t+O(\Delta t) .\]
\(\xi\)是随机变量,对随机变量的撒点平均得到主方程的结果。这里假设态受随机算符\(A \xi(t)\)影响:
\[\quad \frac{d}{d t}|\psi(t)\rangle=i A \xi(t)|\psi(t)\rangle .\]
为了实现方程([eq1])的要求:
\[\begin{aligned} & \operatorname{Av}_{\xi}|\psi(t+\Delta t, \xi)\rangle\langle\psi(t+\Delta t, \xi)|=|\psi(t)\rangle\langle\psi(t)| \\ & +\operatorname{Av}_{\xi}\left(i A \int_t^{t+\Delta t} \xi(\tau) d \tau|\psi(t)\rangle\langle\psi(t)|-i|\psi(t)\rangle\langle\psi(t)| A \int_t^{t+\Delta t} \xi(\tau) d \tau\right) \\ & +\operatorname{Av}_{\xi}\left[\int_t^{t+\Delta t} \int_t^{t+\Delta t} \xi(\tau) \xi\left(\tau^{\prime}\right) d \tau d \tau^{\prime}\left(A|\psi(t)\rangle\langle\psi(t)| A-\frac{A^2}{2}|\psi(t)\rangle\langle\psi(t)|-|\psi(t)\rangle\langle\psi(t)| \frac{A^2}{2}\right)\right]\\\ &+O\left(\Delta t^2\right) . \end{aligned}\]
如果要求随机变量\(\operatorname{Av}_{\xi} \xi(\tau)=0\),并且关联函数也可以要求为:
\[C(t) \equiv \int_t^{t+\Delta t} \int_t^{t+\Delta t} \xi(\tau) \xi\left(\tau^{\prime}\right) d \tau d \tau^{\prime}= \delta(t)\]
则原式化简为:
\[\begin{aligned} & \operatorname{Av}_{\xi}|\psi(t+\Delta t, \xi)\rangle\langle\psi(t+\Delta t, \xi)|=|\psi(t)\rangle\langle\psi(t)| \\ & +\left(A|\psi(t)\rangle\langle\psi(t)| A-\frac{A^2}{2}|\psi(t)\rangle\langle\psi(t)|-|\psi(t)\rangle\langle\psi(t)| \frac{A^2}{2}\right) \Delta t+O\left(\Delta t^2\right) . \end{aligned}\]
对比Lindblad方程得\(A = \sqrt{\gamma_k} L_k\),写出改写后的方程:
\[\label{eq2} \frac{d}{d t}|\psi(t)\rangle=-i\left(H-\sum_k L_k \xi_k(t)\right)|\psi(t)\rangle,\]
其中随机变量满足:
\[\begin{aligned} &\operatorname{Av}_{\xi} \xi_k(t) \xi_m\left(t^{\prime}\right)=\delta_{k m} \delta\left(t-t^{\prime}\right) \sqrt{\gamma_k} .\\ &\operatorname{Av}_{\xi}|\psi(T, \xi)\rangle\langle\psi(T, \xi)|=\rho(T) \end{aligned}\]
与前文中测量部分的随机主方程有一点相似但还差一点,前文为了方便叙述没有讲明两种随机变量之间的关系,(Wiener noise和Stratonovich noise)实际上有转换关系,Wiener噪声实际上是一种对噪声模型的简化,任意状态下的系统都经历着瞬变的,同质的噪声,本身就是一件不那么合理的事,观察方程([eq2]),实际上的受到的噪声会随着系统的状态的变化而变化,\(L_k \xi_k(t)\)作用于\(|\psi(t)\rangle\) 的结果会随着系统\(|\psi(t)\rangle\) 而变化。
\[\begin{gathered} \tilde{\int_0^t} g(x(t), t) d W_{\xi}=\int_0^t g(x(t), t) d W+\frac{1}{2} \int_0^t \frac{\partial g(x(t), t)}{\partial x} g(x(t), t) d t . \\ d y=\left[f+\frac{g}{2} \frac{\partial g}{\partial y}\right] d t+g d W . \end{gathered}\]
积分号上的波浪线用于区分tratonovich noise的积分, 放在线性空间中有:
\[d x_i=\left(A_i+\frac{1}{2} \sum_{j=1}^N \sum_{k=1}^N B_{k j} \frac{\partial B_{i j}}{\partial v_k}\right) d t+\sum_{j=1}^N B_{i j} d W_j \quad \text { (Ito). }\]
其中\(A_i\)表示原tratonovich积分中的固定项,而\(B\)是两种随机变量的转换矩阵,通过这种方式tratonovich积分 实现向Ito积分的转换。直接将结果写成伊藤积分的形式(这里为了对比设L算符厄米,实际上不厄米能够得到更广泛形式 的随机主方程):
\[\quad d|\psi\rangle=(-iH+\sum_{}^{k}\frac{\gamma_k}{2} L^2 d t- \sqrt{\gamma_k} L d W)|\psi\rangle\]
这里的\(dW\)为Wiener微元,满足之前的条件,写成主方程的形式:
\[\label{eq3} \begin{aligned} d \rho &= i[H,\rho]dt -\frac{\gamma_k}{2}[L_k,[L_k, \rho]] d t + \sqrt{\gamma_k}(L_k \rho+\rho L_k) d W \\ &= \mathcal{L}(\rho) + \sqrt{\gamma_k}(L_k \rho+\rho L_k) d W \end{aligned}\]
加入随机过程后,主方程的演化可以看作态始终在做期望值为0的连续测量,实际上是为了形式统一,方程([eq3])加入了一个随机项,引入的额外项在多次平均之后 能够被消去,即:
\[\operatorname{Av}(\sqrt{\gamma_k}(L_k \rho+\rho L_k) d W) = 0\]
连续测量的过程和开放系统的演化形式上是统一的,区别在于随机项的影响。
QUANTUM MEASUREMENT AND CONTROL
Howard M Wiseman, Gerard J Milburn
.
QUANTUM MEASUREMENT THEORY AND ITS APPLICATIONS
Kurt Jacobs
.
Lecture Notes on the Theory of Open Quantum Systems
Daniel A. Lidar
2020 (arXiv:1902.00967).

Decoherence, Einselection, and the Quantum Origins of the Classical
Wojciech H. Zurek
Reviews of Modern Physics, 2003, 75 (3), 715–775.
DOI: 10.1103/RevModPhys.75.715
Stochastic Processes for Physicists: Understanding Noisy Systems
Kurt Jacobs
2010.
DOI: 10.1017/CBO9780511815980
Suppressing Quantum Errors by Scaling a Surface Code Logical Qubit
Rajeev Acharya, Igor Aleiner, Richard Allen, Trond I. Andersen, Markus Ansmann, Frank Arute, Kunal Arya, Abraham Asfaw, Juan Atalaya, Ryan Babbush, Dave Bacon, Joseph C. Bardin, Joao Basso, Andreas Bengtsson, Sergio Boixo, Gina Bortoli, Alexandre Bourassa, Jenna Bovaird, Leon Brill, Michael Broughton, Bob B. Buckley, David A. Buell, Tim Burger, Brian Burkett, Nicholas Bushnell, Yu Chen, Zijun Chen, Ben Chiaro, Josh Cogan, Roberto Collins, Paul Conner, William Courtney, Alexander L. Crook, Ben Curtin, Dripto M. Debroy, Alexander Del Toro Barba, Sean Demura, Andrew Dunsworth, Daniel Eppens, Catherine Erickson, Lara Faoro, Edward Farhi, Reza Fatemi, Leslie Flores Burgos, Ebrahim Forati, Austin G. Fowler, Brooks Foxen, William Giang, Craig Gidney, Dar Gilboa, Marissa Giustina, Alejandro Grajales Dau, Jonathan A. Gross, Steve Habegger, Michael C. Hamilton, Matthew P. Harrigan, Sean D. Harrington, Oscar Higgott, Jeremy Hilton, Markus Hoffmann, Sabrina Hong, Trent Huang, Ashley Huff, William J. Huggins, Lev B. Ioffe, Sergei V. Isakov, Justin Iveland, Evan Jeffrey, Zhang Jiang, Cody Jones, Pavol Juhas, Dvir Kafri, Kostyantyn Kechedzhi, Julian Kelly, Tanuj Khattar, Mostafa Khezri, M'aria Kieferov'a, Seon Kim, Alexei Kitaev, Paul V. Klimov, Andrey R. Klots, Alexander N. Korotkov, Fedor Kostritsa, John Mark Kreikebaum, David Landhuis, Pavel Laptev, Kim-Ming Lau, Lily Laws, Joonho Lee, Kenny Lee, Brian J. Lester, Alexander Lill, Wayne Liu, Aditya Locharla, Erik Lucero, Fionn D. Malone, Jeffrey Marshall, Orion Martin, Jarrod R. McClean, Trevor McCourt, Matt McEwen, Anthony Megrant, Bernardo Meurer Costa, Xiao Mi, Kevin C. Miao, Masoud Mohseni, Shirin Montazeri, Alexis Morvan, Emily Mount, Wojciech Mruczkiewicz, Ofer Naaman, Matthew Neeley, Charles Neill, Ani Nersisyan, Hartmut Neven, Michael Newman, Jiun How Ng, Anthony Nguyen, Murray Nguyen, Murphy Yuezhen Niu, Thomas E. O'Brien, Alex Opremcak, John Platt, Andre Petukhov, Rebecca Potter, Leonid P. Pryadko, Chris Quintana, Pedram Roushan, Nicholas C. Rubin, Negar Saei, Daniel Sank, Kannan Sankaragomathi, Kevin J. Satzinger, Henry F. Schurkus, Christopher Schuster, Michael J. Shearn, Aaron Shorter, Vladimir Shvarts, Jindra Skruzny, Vadim Smelyanskiy, W. Clarke Smith, George Sterling, Doug Strain, Marco Szalay, Alfredo Torres, Guifre Vidal, Benjamin Villalonga, Catherine Vollgraff Heidweiller, Theodore White, Cheng Xing, Z. Jamie Yao, Ping Yeh, Juhwan Yoo, Grayson Young, Adam Zalcman, Yaxing Zhang, Ningfeng Zhu, Google Quantum AI
Nature, 2023, 614 (7949), 676–681.
DOI: 10.1038/s41586-022-05434-1
Open Quantum Systems. An Introduction
'Angel Rivas, Susana F. Huelga
2012.
DOI: 10.1007/978-3-642-23354-8